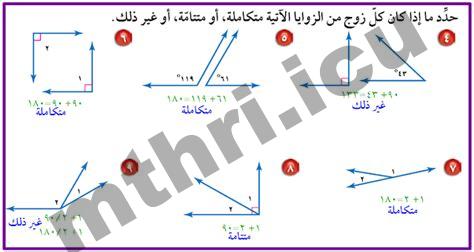
السؤال هو : أزواج الزوايا المتكاملة هي.
الإجابة الصحيحة هي : زاويتان قائمتان، زاوية حادة بزاوية منفرجة، زاوية منفرجة بزاوية حادة .
أزواج الزوايا المتكاملة هي
في الهندسة، يتم تعريف زوج الزوايا المتكاملة على أنهما زاويتان متجاورتان مجموعهما 180 درجة. وبعبارة أخرى، فهما زاويتان متاخمتان تشكلان خطًا مستقيمًا. للأزواج المتكاملة العديد من التطبيقات في الهندسة والرياضيات، بما في ذلك تحديد أطوال الأضلاع والزوايا في المثلثات والمضلعات الأخرى.
أنواع الأزواج المتكاملة
هناك ثلاثة أنواع رئيسية من الأزواج المتكاملة:
الزوايا المتجاورة: زاويتان متجاورتان على نفس الخط المستقيم وتتشكلان من تقاطع خطين.
الزوايا المتقابلة: زاويتان متقابلتان في رؤوس متقابلة من شكل رباعي.
الزوايا المتناظرة: زوجان من الزوايا المتقابلة والمتساوية في شكل رباعي.
خصائص الأزواج المتكاملة
للأزواج المتكاملة العديد من الخصائص المهمة، منها:
مجموع زاويتين متكاملتين يساوي 180 درجة.
الزوايا المقابلة في شكل رباعي متكاملة.
الزوايا المتناظرة في شكل رباعي متكاملة.
إثبات مجموع زاويتين متكاملتين
يمكن إثبات أن مجموع زاويتين متكاملتين يساوي 180 درجة باستخدام مسلمة زوايا قائمة. فإذا افترضنا أن لدينا زاويتين متكاملتين ∠A و∠B، فإنهما تشكلان خطًا مستقيمًا. يمكننا رسم زاوية قائمة ∠C بحيث تكون متاخمة لـ∠A. نظرًا لأن مجموع الزوايا المتجاورة ∠A و∠C يساوي 90 درجة، فإن مجموع ∠A و∠B يساوي 180 درجة.
تطبيقات الأزواج المتكاملة
للأزواج المتكاملة العديد من التطبيقات في الهندسة والرياضيات، منها:
إيجاد أطوال الأضلاع والزوايا في المثلثات والمضلعات الأخرى.
تحديد مواضع النقاط على المستوى.
حساب المساحات والحجوم.
أمثلة على الأزواج المتكاملة
فيما يلي بعض الأمثلة على الأزواج المتكاملة:
الزوايا المتجاورة في مربع.
الزوايا المتقابلة في مستطيل.
الزوايا المتناظرة في متوازي الأضلاع.
التاريخ
يعود مفهوم الأزواج المتكاملة إلى الرياضيات اليونانية القديمة. فقد كان الإغريق على دراية بهذه الخاصية واستخدموها لحل مجموعة متنوعة من المشكلات الهندسية. تم تدوين مفهوم الأزواج المتكاملة لأول مرة في كتاب “العناصر” لإقليدس، الذي كتبه حوالي 300 قبل الميلاد.
الأزواج المتكاملة هي مفهوم مهم في الهندسة والرياضيات ولها العديد من التطبيقات. عن طريق فهم خصائص وإثباتات الأزواج المتكاملة، يمكننا حل مجموعة واسعة من المشكلات الهندسية بدقة وفعالية.